TEORÍA DE LA PROBABILIDAD: El Teorema de Bayes y la inferencia a la mejor explicación.
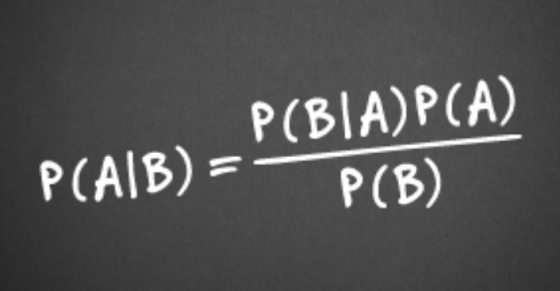
El teorema de Bayes, nombrado después del matemático inglés
Thomas Bayes (1701-1761), es una manera de calcular la probabilidad
condicional, es decir, la probabilidad de que ocurra un acontecimiento dado
condiciones específicas. Por ejemplo, la probabilidad de encontrar un espacio de
estacionamiento seguramente estaría vinculada a la hora del día a la que quiero
aparcar, donde quiero hacerlo, y qué eventos están ocurriendo en ese momento.
El teorema de Bayes es una manera útil en la que los
teóricos de la probabilidad son capaces de calcular la probabilidad de
declaraciones o acontecimientos particulares. Utilizando el teorema, las
probabilidades calculadas oscilarán entre los valores 0 y 1. 1 representa la
probabilidad más alta posible y 0 la probabilidad más baja posible. Si se
calcula un valor superior a 0,5 (> 0,5), entonces se indica una probabilidad
positiva de una sentencia o evento, mientras que un cálculo de menos de 0,5
(<0,5) sugiere una improbabilidad. 0,5 sugeriría un equilibrio exacto entre
los dos. Según la fórmula, la probabilidad de un evento o una sentencia se
designa como Pr (A.B) (1). Esto
indica la probabilidad de un evento o declaración de A dado B, o A en B con A y
B permaneciendo para declaraciones específicas o eventos. También es importante
observar que es imposible calcular la probabilidad con absoluta precisión y
certidumbre. Por lo tanto, es mejor utilizar frases como "altamente probable"
(>> .5) o "altamente Improbable" (<< .5) al argumentar
por una hipótesis, y que una hipótesis es más probable que las hipótesis rivales.
 |
| Otra manera de formular el Teorema de Bayes. |
Los enfoques bayesianos se usan con frecuencia en la
teología y la filosofía de la religión, especialmente cuando se trata de
argumentos para la existencia de Dios, calculando la existencia de Dios, el
problema del mal y el problema de los milagros. Según Chris Wiggins, profesor
asociado de matemáticas aplicadas en la Universidad de Columbia: "los argumentos que emplean el teorema
de Bayes calculan la probabilidad de que Dios dadas nuestras experiencias en el
mundo (la existencia del mal, las experiencias religiosas, etc.) y asignan
números a la probabilidad de estos hechos dada la existencia o inexistencia de
Dios, así como a la creencia previa de la existencia de Dios -la probabilidad
que asignaríamos a la existencia de Dios si no tuviéramos datos de nuestras
experiencias" (2).
 |
| Richard Swinburne, profesor emérito de filosofía en la Universidad de Oxford. Reconocido por su trabajo dentro de la teología natural. |
En su libro ”La Resurrección de Dios encarnado”, el filósofo
Richard Swinburne, en su aplicación de los cálculos bayesianos, estimó la
probabilidad de que la resurrección de Jesús estuviera en un alto 97%, por lo
que es altamente probable (3). Hay
una serie de valores que Swinburne utilizó en su cálculo bayesiano, por
ejemplo, pesa mucho sobre cómo vivió Jesús, una pieza clave de evidencia que él
sostiene es muy relevante para saber si debemos creer que resucitó de entre los
muertos. Swinburne también influye en la evidencia que apoya la resurrección de
Jesús, que la evidencia que poseemos (la diversidad de las apariencias de la
resurrección, tumba vacía, etc.) es el tipo de evidencia que esperaríamos si
Jesús realmente resucitase de entre los muertos.
El filósofo William Craig
argumenta de manera similar preguntando: "¿Cuál sería la probabilidad de
que la resurrección no ocurriera en retrospectiva de estos cuatro hechos?"
A lo cual él responde que "Es muy, altamente, muy improbable que debamos
tener esa evidencia [cuatro hechos] si la resurrección no hubiera ocurrido" (4). Sin embargo, no todos
los eruditos cristianos han encontrado los cálculos bayesianos de Swinburne, y
los valores que le asigna, necesariamente convincentes (5). Del mismo modo, naturalistas como John Mackie y Richard
Dawkins han intentado utilizar cálculos bayesianos para refutar o argumentar
contra la existencia de Dios.
Inferencia
a la mejor explicación:
Una alternativa al razonamiento bayesiano es lo que se
conoce como la inferencia a la mejor explicación. Esto comienza con la
necesidad y el deseo de ser capaz de explicar los datos. Con el fin de explicar
los datos reunimos un conjunto de opciones que tratan de dar cuenta de ello. De
la lista de opciones se selecciona una explicación que, diríamos, tiende a
explicar mejor los datos. Esta es una práctica muy común que la mayoría de
nosotros usamos diariamente cuando tratamos con hipótesis que podrían explicar
algunos fenómenos u otros.
Por ejemplo, si Jill pone su dinero en el alféizar de la
ventana, sale de su habitación y luego regresa para encontrarla, probablemente
tendrá varias hipótesis para explicar el fenómeno de su desaparición. Si la
ventana sobre el alféizar de la misma está entreabierta, podría sospechar que
alguien saltó sobre su pequeña valla de jardín, puso una mano a través de la
ventana y salió con su dinero. Alternativamente, alguien dentro de la casa, tal
vez un compañero de piso en una de las habitaciones adyacentes se podría haber
colado y robado. Sin embargo, el que Jill haya cerrado la puerta del dormitorio
con una llave, la única llave que coincide con la cerradura, hace que de ello una
explicación poco probable. Tal vez fue la trabajadora doméstica, pero la
trabajadora doméstica estaba en la habitación de Jill sólo una vez ese día y
una hora antes de que pusiera su dinero en el alféizar de la ventana. Jill se
presenta con una serie de opciones que buscan explicar la desaparición de su
dinero.
El filósofo Gilbert Harman explica que "en general, habrá varias hipótesis que podrían explicar la
evidencia, por lo que uno debe ser capaz de rechazar todas esas hipótesis
alternativas antes de que se justifique hacer la inferencia. De este modo se
infiere, desde la premisa de que una hipótesis dada proporcionaría una
"mejor" explicación de la evidencia que cualquier otra hipótesis,
hasta la conclusión de que la hipótesis dada es verdadera " (6).
Así, con Jill, ella tiene un conjunto de tres opciones para
explicar la posible razón detrás de su dinero perdido. Ella descarta la
posibilidad de que un compañero de casa lo robe dada la puerta cerrada. Tampoco
es posible que la trabajadora doméstica sea el ladrón culpable dado que el
trabajador no estaba en la habitación en el momento en que desapareció el
dinero. La opción más viable, con estos otros dos descartados, es que alguien
puso una mano a través de la ventana abierta no sólo aparentemente evidenciada
por la ventana abierta en sí, sino también por la incapacidad de las otras
opciones para dar sentido a la situación.
Los criterios utilizados para
determinar qué opción en un conjunto de opciones es el mejor, es debatido. Por
ejemplo, como hemos examinado antes en un ensayo separado, muchos sostienen que
las propiedades tales como el poder explicativo, el alcance explicativo, la
plausibilidad, el ad hoc-etc. son buenos medios para llegar a una mejor
explicación (7). Sin embargo, como
se ha observado, la inferencia a la mejor explicación no es inmune al error (8). Sólo porque una explicación propuesta
parece ser capaz de explicar mejor los fenómenos, no garantiza que sea
verdadera. Después de todo, podría ser el caso de que las opciones en sí no son
exhaustivas y que la verdadera explicación sigue siendo desconocido (tal vez
una cuarta opción para dar cuenta del dilema de Jill es que el viento sopló el
dinero fuera de la ventana y debajo de su mesa, una hipótesis que no había
entretenido que podría muy bien ser cierto). Sin embargo, como explica C. Behan
McCullagh en su libro Justifying Historical Descriptions, si una explicación o
reconstrucción histórica (si queremos inferir la mejor explicación de un evento
en el pasado), supera otras explicaciones competitivas, entonces es probable
que ser verdad, y que debamos aceptarlo como verdadero a menos que nueva
evidencia sugiera lo contrario (9).
Referencias:
1. Stuart,
A. 1994. Kendall’s Advanced Theory of Statistics: Volume I—Distribution Theory.
p. 294, 300.
2. Wiggins,
C. What is Bayes’s theorem… Disponible.
3. Otte, R.
The Resurrection of God Incarnate Review. Disponible.
4.
Swinburne, R. 2003. The Resurrection of God Incarnate. p. 3.
5. Otte, R.
Ibid.
6. Gilbert
Harman quoted by The Information Philosopher. Disponible.
7. Craig,
W. 2012. Stephen Law on the Non-existence of Jesus of Nazareth. Disponible.
8. Craig,
W. 2008. Reasonable Faith (3rd ed.). p. 92 (Scribd ebook format)
9.
McCullagh, B. 1984. Justifying Historical Descriptions. p. 19.
Traducción y edición: Alan Peña

Comentarios
Publicar un comentario